- Forfatter Matthew Elmers [email protected].
- Public 2023-12-16 22:28.
- Sist endret 2025-01-24 09:32.

Hva bestemmer nøyaktigheten - en av hovedtrekkene til et våpen? Tydeligvis av kvaliteten på fatet og kassetten. La oss utsette patronen for nå, men vurder prosessens fysikk.
Ta en metallstang eller et rør laget av elastisk metall og fest det stivt i en massiv base. Så vi får en modell av enheten som studeres. Nå, hvis vi treffer stangen, spiller det ingen rolle på hvilket sted og i hvilken retning, enten trekke den tilbake eller klemme den, eller til slutt sette en patron inn i røret og skyte et skudd, vi vil se at stangen (fat) har kommet inn i en dempet oscillerende bevegelse. Disse vibrasjonene brytes ned til det enkleste, og hver type så enkel vibrasjon av fatet vil påvirke nøyaktigheten (nøyaktigheten) av skytingen på sin egen måte.
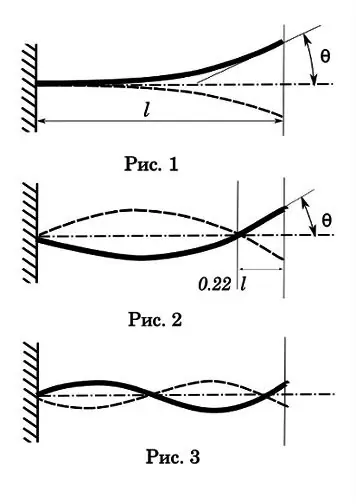
La oss begynne med første orden eller pitch vibrasjoner. Som du kan se (fig. 1), har en slik svingning bare en node ved festepunktet, den største amplituden, den lengste forfallstiden og den lengste svingningstiden i en periode. Denne tiden er 0,017-0,033 sek. Kule reisetid gjennom boringen er 0, 001-0, 002 sek. Det vil si betydelig mindre enn syklusen til en oscillasjon, noe som betyr at denne typen oscillasjon ikke har en signifikant effekt på nøyaktigheten til et enkelt skudd. Men med automatisk fotografering kan et interessant bilde vise seg. La oss si at brannhastigheten er 1200 rds / min, dvs. tid for en syklus - 0,05 sek. Med en førsteordens oscillasjonsperiode på 0, 025 sek, har vi et frekvensforhold på flere måter. Og dette er en uunnværlig betingelse for resonans med alle konsekvensene som følger - våpenet begynner å riste med så stor kraft at det kan falle fra hverandre.
La oss gå videre til svingninger av andre orden (fig. 2). Men jeg foreslår at humaniora -studenter først gjennomfører et eksperiment for å eliminere manglene ved utdanning innen fysikk. Du må ta en liten gutt (du kan en jente), sette ham på en sving og svinge. Før du er en pendel. Stå på siden av svingen og prøv å slå gutten med ballen. Etter en rekke forsøk kommer du til den konklusjonen at den beste måten å treffe er når målet er i den første oscillasjonsfasen - maksimal avvik fra likevektspunktet. På dette tidspunktet har målet null hastighet.
La oss se på andre ordens diagram. Den andre vibrasjonsnoden er plassert omtrent 0,22 fra enden av fatet. Dette punktet er en naturlov, det er umulig å lage slike vibrasjoner for utliggerstrålen slik at den andre noden faller på den frie enden. Det er der det er og avhenger ikke av lengden på fatet.
Oscillasjonsamplituden for andreordens ordning er lavere, men oscillasjonstiden er allerede sammenlignbar med tidspunktet for kulen gjennom hullet-0, 0025-0, 005 sek. Så for enkeltskyting er dette allerede av interesse. For å gjøre det klart hva vi snakker om, tenk deg et fat som er 1 meter langt. Kulen beveger seg gjennom hele fatet på 0, 001 sekunder. Hvis oscillasjonsperioden er 0,004 sek., Når kulen forlater fatet, vil fatet nå sin maksimale bøyning i den første fasen. Spørsmålet til humaniora er - på hvilket tidspunkt (i hvilken fase) er det best å skyte en kule ut av fatet for å sikre konsekvens av resultatene? Husk svingen. På nullpunktet er vektoren for stammens nedbøyningshastighet maksimal. Det er vanskeligere for en kule å treffe dette punktet på fatskåret, den har også sin egen feil i hastigheten. Det vil si at det beste øyeblikket for kulen å fly ut vil være når fatet er på det høyeste punktet i den første nedbøyningsfasen - som på figuren. Da vil ubetydelige avvik i kulehastigheten bli kompensert av lengre tid som tønnen bruker i sin mest stabile fase.
En grafisk fremstilling av dette fenomenet kan tydelig sees i diagrammet (fig. 4-5). Her - Δt er tidsfeilen som kulen krysser munnstykket på fatet. I fig. 4 er ideell når den gjennomsnittlige starttiden for kuler faller sammen med nullfasen i fatoscillasjonen. (Matematikere! Jeg vet at hastighetsfordelingen er ikke-lineær.) Det skyggelagte området er spredningsvinkelen til banene.
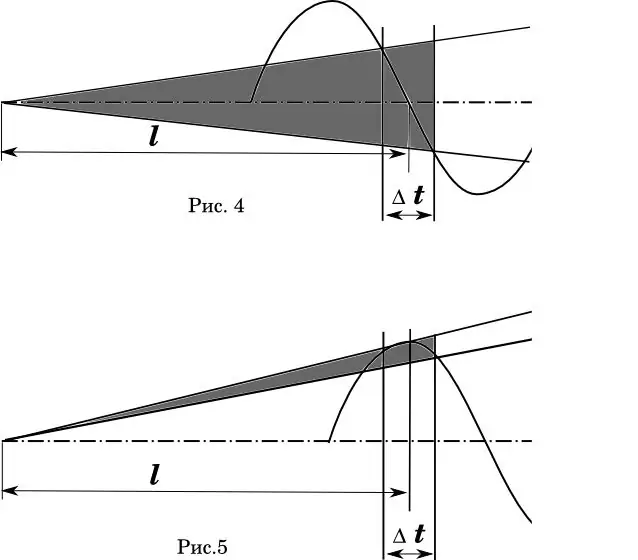
I figur 5 forblir fatlengden og hastighetsfeilen den samme. Men fasen i fatbøyningen forskyves slik at gjennomsnittlig avgangstid faller sammen med den maksimale nedbøyningen av fatet. Er kommentarer overflødige?
Vel, er det verdt lyset? Hvor alvorlige kan avvikene forårsaket av andreordens svingninger være? Alvorlig og veldig alvorlig. I følge den sovjetiske professoren Dmitry Aleksandrovich Ventzel ble følgende resultater oppnådd i et av forsøkene: medianavvikets radius økte med 40% med en endring i fatlengden med bare 100 mm. Til sammenligning kan en fatbehandling av høy kvalitet forbedre nøyaktigheten med bare 20%!
La oss nå se på formelen for vibrasjonsfrekvensen:
hvor:
k - koeffisient for andreordens svingninger - 4, 7;
L er fatlengden;
E er elastisitetsmodulen;
Jeg er seksjonens treghetsmoment;
m er massen til stammen.
… og fortsett til analysen og konklusjonene.
Den åpenbare konklusjonen fra figur 4-5 er kulehastighetsfeil. Det avhenger av kvaliteten på pulveret og dets vekt og tetthet i patronen. Hvis denne feilen er minst en fjerdedel av syklusen, kan alt annet bli gitt opp. Heldigvis har vitenskap og industri oppnådd veldig stor stabilitet i denne saken. Og for de mer sofistikerte (for eksempel benkestøtte) er det alle betingelser for selvmontering av patroner for å justere kulens frigjøringsfase nøyaktig til fatlengden.
Så vi har en patron med lavest mulig hastighetsvariasjon. Fatlengden ble beregnet ut fra maksimalvekten. Spørsmålet om stabilitet melder seg. Vi ser på formelen. Hvilke variabler påvirker endringen i oscillasjonsfrekvensen? Fatlengde, elastisitetsmodul og masse. Tønnen varmes opp under avfyring. Kan varme endre fatlengde slik at nøyaktigheten påvirkes. Ja og nei. Ja, siden dette tallet ligger innenfor hundredeler av en prosent for en temperatur på 200 C. Nei, siden endringen i stålets elastiske modul for den samme temperaturen er omtrent 8-9%, for 600C er det nesten to ganger. Det vil si mange ganger høyere! Tønnen blir mykere, bøyefasen til fatet forskyves fremover i det øyeblikket kulen forlater, og nøyaktigheten synker. Hva sier en gjennomtenkt analytiker? Han vil si at det er umulig å få maksimal nøyaktighet på en fatlengde i kald og varm modus! Våpenet kan ha en bedre ytelse med enten en kald eller varm tønne. Følgelig oppnås to klasser av våpen. Den ene er for bakholdsaksjoner, når målet må treffes fra det første - "kalde" skuddet, fordi nøyaktigheten til det andre vil bli verre på grunn av den uunngåelige oppvarmingen av fatet. I et slikt våpen er det ikke noe presserende behov for automatisering. Og den andre klassen er automatiske rifler, lengden på fatet er justert til det varme fatet. I dette tilfellet kan en mulig glipp på grunn av den lave nøyaktigheten til et kaldt skudd kompenseres for et raskt etterfølgende varmt og mer nøyaktig skudd.
EF Dragunov kjente fysikken i denne prosessen veldig godt da han designet riflet. Jeg foreslår at du gjør deg kjent med historien om sønnen Alexei. Men først må noen bryte hjernen. Som du vet, nærmet to prøver av Konstantinov og Dragunov finalen i konkurransen om et snikskytterrifle. Designerne var venner og hjalp hverandre i alt. Så Konstantinovs rifle var "innstilt" på kald modus, Dragunovs rifle til "varmt". I et forsøk på å forbedre nøyaktigheten til rivalens rifle, skyter Dragunov riflet med lange pauser.

La oss se på formelen igjen. Som du kan se, avhenger frekvensen også av fatets masse. Massen på stammen er konstant. Men hard kontakt med forenden gir en uforutsigbar positiv tilbakemelding til fatet. Systemet-fat-forend-arm (støtte) vil ha et annet treghetsmoment (et sett med masser i forhold til festepunktet), noe som betyr at dette også kan forårsake et faseskift. Det er derfor idrettsutøvere bruker myk støtte. Den samme egenskapen er knyttet til anvendelsen av prinsippet om "suspendert fat", når våpenets forkant ikke har en hard kontakt med fatet og er stift festet til det (våpenet) bare i området av mottaker, og den andre enden enten ikke berører tønnen i det hele tatt eller berører gjennom en fjærbelastet ledd (SVD).
Endelig tanke. Det faktum at med samme fatlengde er det umulig å oppnå samme nøyaktighet ved forskjellige temperaturer, gir en utmerket grunn til å strekke hjernen din. Det er bare nødvendig å endre lengden og / eller massen på fatet når temperaturen på fatet endres. Uten å endre verken lengden eller vekten på fatet. Sett fra humaniora er dette et paradoks. Sett fra en tekniker, en ideell oppgave. Hele livet til en designer er knyttet til løsningen av slike problemer. Sherlockene hviler.






